前言
这一节主要理解什么呢,要理解的是计算机里面存储数据都是有一个无形的容器的,计算机中存储的数据最终都是二进制存储的,每个容器都有最大容量,比如有的可以装 4 个二进制数,有的可以装 8 个二进制数,但其实归根到底,还是寄存器的宽度导致了存在数据宽度,要是寄存器有 5 位的,7 位的,那么肯定就会有相应的数据宽度,由于数据宽度的存在,数据运算就和个圈一样,下面会给出具体的图
符号问题的话,记住这一点:计算机只会做加减法,至于补码,反码啥的都是人去规定的,这个要结合之后的 JCC 才能彻底理解带符号的运算问题
因为计算机做任何运算,都需要先将数据存到某数据宽度的寄存器中,所以一定要指明数据宽度!!
课堂
总述
以前我们只是记忆过如果计算机中某容器只能存储 4 位二进制数,那么如果存无符号数,那四个位都可以存数,则一共十六种情况,0000 到 1111(24);如果存储有符号数,则最高位要被当做符号位,如果为 0 则为正数,如果为 1 则为负数,所以此时只能后三位用来表示数据值,则有正 000 到 111(23)和负 000 到 111。但是计算机真的认识有没有符号吗???而且我们平时说的反码,原码,补码,计算机不知道,这只是人们总结出来的规律
4 位宽度表示
实际上计算机中没有 4 位容器,我们只是为了引入方便理解,汇编中最小的容器数据宽度是 8 位的,即一个字节
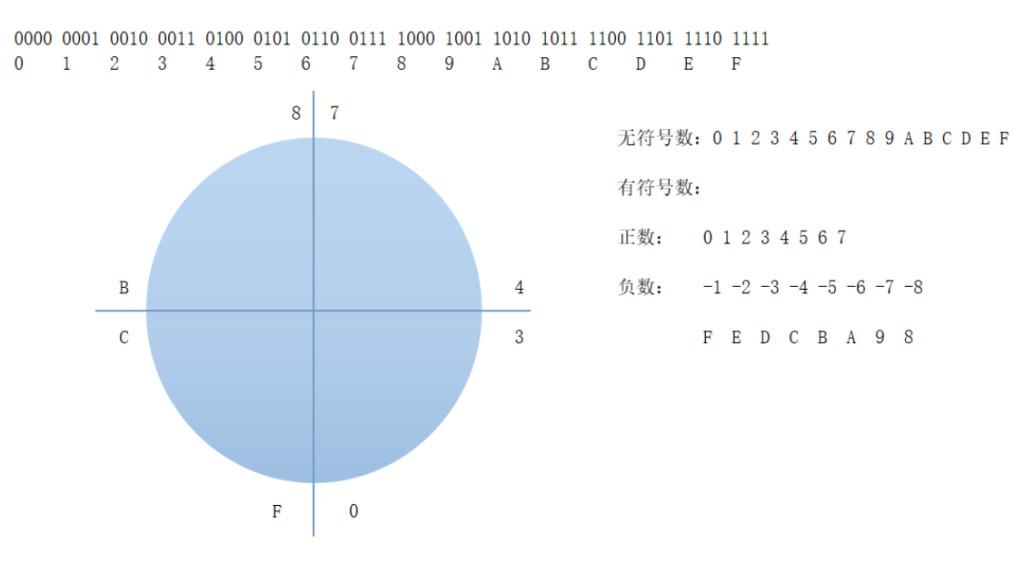
- 假设计算机只能存储 4 位二进制数:一共有 16 种数可以存:换成十六进制刚好是 0 到 F
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
0 1 2 3 4 5 6 7 8 9 A B C D E F
-
无符号数:至于这块容器到底存有符号还是无符号数,是我们定义的。计算机最终只认识 0、1,它不管哪个正负。所以现在如下图所示,从圆的右下方开始存数据,存无符号数。依次存 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F。如果再比 F 大的数则会变成 0!此时一共可以存 16 种数
-
有符号数:由于只能存 4 位二进制数,现在我们又有存负数的需求,怎么办呢?公平起见,分两半,约定好一半存正数,一半存负数,所以此时 0 到 7 是正数,8 到 F 是负数。因为数字只能用 4 位来存储,又要表示负数又要表示正数,所以干脆分一半。如果换成二进制就会发现,0 到 7 最高位全是 0;8 到 F 最高位全是 1。而且此时 F 为最大的负数,怎么推断的的呢?因为如果比 F 再大 1 的数就变成了 0:1111+1=10000,只能存 4 位,多出来的位,计算机会丢弃,则计算机会当做 0000,即 0。所以 F 是最大的负数-1。那么对应的 E 就是-2,D 就是-3。(这里可以用补码去理解)
- 有符号数二进制 1111 表示最大的负数-1,现在用补码转原码的知识(计算机中的数都是二进制补码的形式存储的):将有符号数 1111(补码)化成十进制是多少:先除符号位取反码 1000,再末位+1,1001。最高位为符号位,后面 001 表示数值,则算出来就是-1(原码)
8 位宽度表示
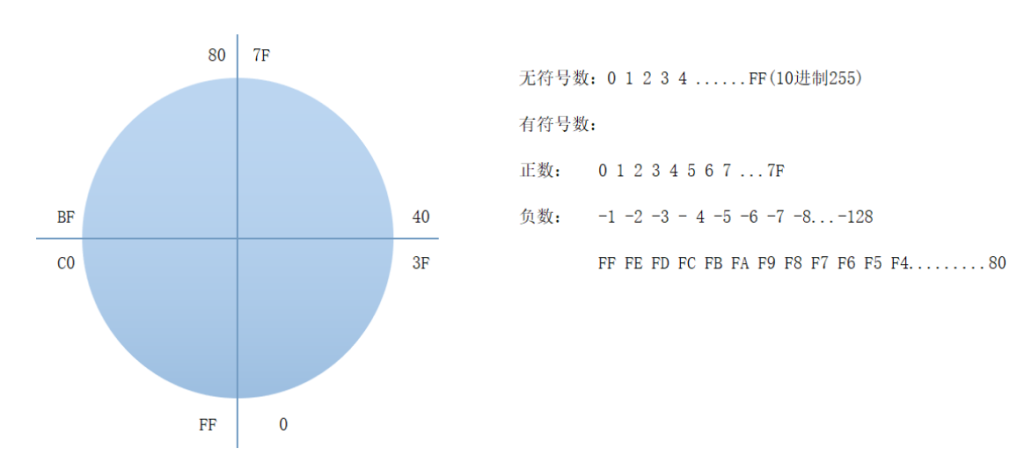
假设现在 4 位不够表示我要存的数了,我换一个大一点的容器,存储数据的范围为 0x00 到 0xFF,即数据宽度为 8 位,那么此时此容器如果用来存无符号数,则可从 0x00 一直存到 0xFF,一共 28=256 种数;如果存有符号数,则还是切一半,00 到 7F 是正数,80 到 FF 为负数,化成二进制可以发现规律,80 到 FF 的最高位都是 1,即最高位为 1 的表示负数。正数同理可得。0xFF 为最大的负数-1,0x80 为最小的负数-128。
16 位宽度表示
-
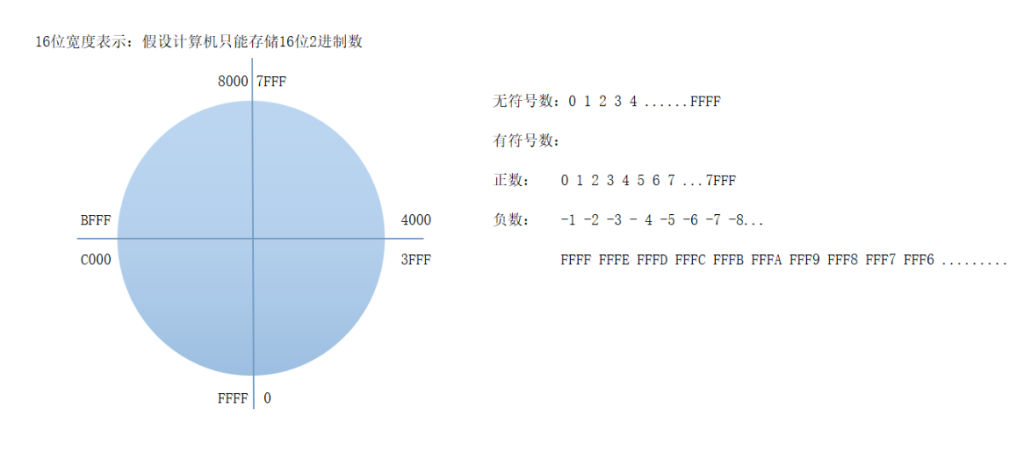
16 位数据宽度容器存储无符号数范围是从 0 到 FFFF
-
存储有符号数从 0 到 7FFF 表示正数,从 8000 到 FFFF 表示负数
32 位宽度表示
目前计算机中最常见的也是这个数据宽度的容器
-
32 位数据宽度容器存储无符号数范围是从 0 到 FFFFFFFF
-
存储有符号数从 0 到 7FFFFFFF 表示正数,从 80000000 到 FFFFFFFF 表示负数

汇编中对应宽度的单位
| name | 中文 | bit | 字节 |
|---|---|---|---|
| BYTE | 字节 | 8bit | 1 字节 |
| WORD | 字 | 16bit | 2 字节 |
| DWORD | 双字 | 32bit | 4 字节 |
存储的数超过了容器的数据宽度
比如一个容器的数据宽度为 4 位,那么如果我现在存一个数 16,化为二进制为 10000,由于只能存 4 位,那么进位的多出来的位会被丢弃,最终读到的是 0000,即 0
逻辑运算
-
如果现在只是将数据存到计算机的容器中,是没有任何意义的,我们还需要告诉计算机这些数据有什么用,让计算机对这些数做运算。所以我们知道计算机到底是如何做运算的,所以我们引入逻辑运算
-
由于计算机受硬件的限制影响,CPU 再复杂可以理解为一条条的线路组成的,而电信号只有两种形式 0 和 1,所以一般计算机的逻辑运算的对象都是二进制数
| 逻辑运算 | 汇编符号 | C 语言符号 | |
|---|---|---|---|
| 或 | or | ||
| 与 | and | & | |
| 异或 | xor | ^ | |
| 非 | not | ! |
加法计算
就是之后衍生出来的任何运算,包括加法减法乘法啦,都能用上面这几种给运算出来,这个在第一篇文章中也展示过一次,我们再来看一下计算机是如何计算 2+3 的,我们如果用汇编语言写 2+3,两个指令就可以搞定,但是对于计算机收到这个指令,计算机只会对以二进制存储的数据做逻辑运算得出结果,而计算机不会做加法运算,就只能这样
#x,y,R为存储数据的容器
2+3
x:0010
y:0011
0010
xor 0011
------------
0001 R:0001
0010
and 0011
------------
0010 <<1 得 0100 #<<1表示左移一位
此时计算机会判断0100是否全为0,如果全为0表示运算结束,将R中此时的值作为结果输出,如果不为0则将R中的值赋给x。0100赋给y再做一次同样运算
0001
xor 0100
-------------
0101 R:0101
0001
and 0100
-------------
0000 <<1 得 0000
判断0000全为0,则运算结束,将R中的值0101作为运算的结果,化成十进制即为5
如何获取某个值的第 N 位是 0 还是 1
比如现在某个寄存器中存了一个值,值化成二进制时,有些特殊的值每一位都有它的特殊含义,所以我们想要知道这个值的第 N 位是 0 还是 1。如果我们把寄存器中的值取出来,一个一个数着看,就会很麻烦,但是如果做下面的运算,就会容易很多:
#现在想要查看某寄存器中的值的第4位是0还是1,我们就可以将寄存器中的值与0x08做与运算,如果得到结果中有一个1,则这个值的第四位就是1,如果结果全是0,则值的第四位就是0
10001111
and 00001000
----------------------
00001000
加密解密
如果进行简单的加密,可以使用亦或运算,因为选择一个双方都知道密钥,用此密钥与数据做亦或加密加密过后,别人如果没有密钥则不好解开这个密文,而对于接受方,使用相同的密钥再做一次亦或即可得到原来的明文值
这里海东老师的例子
要加密的数据:20和15 00100000 00010101
^ 01010100 ^ 01010100
------------ ------------
密钥:54 01110100 01000001
加密后的结果: 74 41
01110100 01000001
^ 01010100 ^ 01010100
------------- ------------
00100000 00010101
解密后的结果: 20 15
作业

1.2-5 等于-3,这个-3 要看存储容器的数据宽度了,如果数据宽度是 8 位,那么刚刚讲过有符号数是这么存储的:FF 是最大的负数-1,那么往前推,FE 表示-2,FD 表示-3,即结果化成十六进制就是 FD,至于最后答案要化成二进制还是八进制,计算机不管,计算机只管将-3 在 8 位宽度的容器中表示为 FD。同理如果是 16 位容器,则结果为 FFFD;32 位容器,则结果为 FFFFFFFD
2.
1000 0111 1010 1101 0110
xor 0101 加密密钥
----------------------------------------------------
1000 0111 1010 1101 0011 加密后的值
xor 0101 解密密钥
-----------------------------------------------------
1000 0111 1010 1101 0110 解密后的值,与原值一致
3.
2-3
假设数据宽度为4bit
-3在计算机中存储方式:先把-3表示出来1011,最高位为符号位,然后除符号位其他位取反最后加1即可(即原码转补码)
所以-3 = 1011 --> 1100 --> 1101 --> D,即计算机收到-3后会将-3用二进制1101存储(数据宽度为4字节)
x:0010
y:1101
0010
xor 1101
----------
1111 R:1111
0010
and 1101
----------
0000 <<1 得0000
所以最终结果为1111,注意这只是计算机存储的形式,十六进制为F
根据计算机底层存储原理可以得到F表示最大的负数-1,可得到答案为-1;也可以通过1111除符号位取反1000,然后+1的1001,也可以得到答案是-1